We usually imagine electric fields as invisible lines in the air, but they can exist inside materials as well. In this exercise you will measure voltages set up by a 9-volt battery in a piece of conductive paper, in order to determine the electric field strength at different points.

Objectives

1. Measure the change in voltage at points along a straight line between two “point charges” (spots of conductive paint on conductive paper)
2. Determine the electric field strength at points along a straight line between the two point charges

Resources

• Voltmeter
  • Video tutorial
• 9-Volt battery
• Wires with alligator clips and metal pushpins
• Paper with conductive paint patterns (2)

The electric field gives the magnitude and direction of the electric force per unit charge at every point in space. Voltage, also referred to as electric potential, is the potential energy per unit charge due to the electric field at a given point. Because the potential energy of a charge moved through an electric field is qE\Delta s, it can be shown that for small distances in an electric field that is changing smoothly E_{avg}\approx \frac{\Delta V}{\Delta s}.

An electric dipole is two equal and opposite point charges. Because electric fields are additive, Coulomb’s Law can be applied to show that the strength of the electric field at a point x along the line joining the two charges of a dipole that are both a distance d from the origin, is E=\frac{qd}{\pi\epsilon_0} \frac{|x|}{(x^2-d^2)^2}.

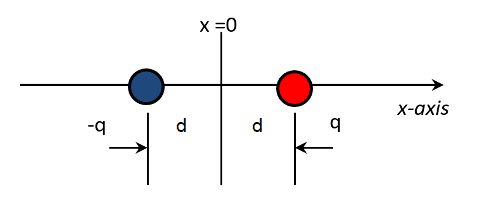
Method:

You can set up an electric field in the paper with conductive patterns by connecting each terminal of the battery to a metal pushpin inserted through the paper and pressing against the conductive paint. You can then use the multimeter to measure potential differences between different points in the paper.