Objectives

• Analyze momentum conservation in a collision between two nearly-frictionless carts on a straight track in three situations:
  • A “bouncy” collision between two carts of equal mass with rubber bumpers
  • A “bouncy” collision between two carts of unequal mass
  • A “sticky” collision between two carts

Resources

• Dynamics cart (2)
• Motion sensors (2)
• Force sensor with rubber bumper (2)
• Cart weights
• ScienceWorkshop interface and DataStudio program
• Modeling clay
• DataStudio setup file momentum.ds

Background

Linear momentum is the product of the mass and velocity of an object. Linear momentum is also a conserved quantity, meaning that if a closed system is not affected by external forces, its total linear momentum cannot change.

The total change in an object’s momentum during a collision is known as the impulse (J). The instantaneous rate of change of an object’s momentum is defined as force. Thus, the impulse on an object is J=\Delta p = \int^{t_f}_{t_i} \vec{F} dt

Although momentum is always conserved in a collision between two isolated objects, some of the energy of movement can be lost through interactions between the objects. A collision in which no energy is lost is termed elastic, otherwise it is inelastic. In any real collision, at least some energy of movement is converted to internal energy and other forms of energy, so no large scale impacts are perfectly elastic. A perfectly inelastic collision is one in which the colliding objects stick together after the collision. It can be shown that the impulse during an elastic collision is twice that if the same collision is perfectly inelastic.

Hints/Guideposts

• If you add weight to a cart, you will want to stick it in place somehow so that it does not shift during collision.
• When colliding two carts in this la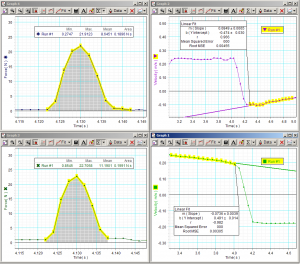b, the motion sensor will not accurately measure the velocity just before or after the collision. This is because it averages over several samples to determine velocity to compensate for interference. This works well for gradual changes in velocity, but for rapid changes in velocity the data become smoothed out. To acccurately determine the velocities, apply a linear fit to the velocity vs. time data before or after the collision, then extrapolate the velocity to the time of the collision, assuming it happens at the midpoint between the maximum and minimum velocities, as shown in the figure.