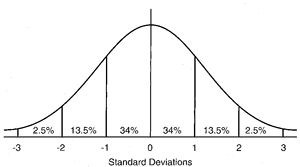
Any time we make a measurement, there is some uncertainty involved. We could try to make our measurement more reliable by repeating it or having others confirm it for us. If we average these measurements together, we expect the average to approach the “true” or “best” value (assuming those are even real things!) as we average more measurements. We also expect the values to be more or less spread out depending on the level of accuracy. This phenomenon is well-described by the Gaussian distribution, or bell curve. The mean (\mu) gives the location of the peak, and the standard deviation (\sigma) describes how wide the curve is.

\mu=\frac{x_1+x_2+\cdots+x_N}{N} \sigma=\sqrt{\frac{1}{N-1} \left[ (x_1-\mu)^2+(x_2-\mu)^2+\cdots+(x_N-\mu)^2 \right] }

The uncertainty in a measured value can be calculated from the standard deviation if multiple measurements are made. This is called by different names depending on the discipline, including standard deviation of the mean, standard error, standard error of the mean.

\mathrm{SDOM}=\sigma/\sqrt{N}

Single Measurements

When making a single measurement, there is no way to calculate standard deviation, so the uncertainty must be estimated. This estimation is based on situational factors such as the skill of the experimenter and/or the reported accuracy of the measuring instrument. In theory, this estimated error is a guess about what the standard deviation of the mean would be if many repeated measurements were made.

Propagating Uncertainty

Often we use two or more experimental values to calculate a third. The amount of uncertainty in the input values should have an effect on the uncertainty of the result. To do this, we use propagation of error. The error propagation formula for some function f of variables x_1, x_2, x_3, … is

\sigma_f=\sqrt{\left(\frac{\partial f}{\partial x_1}\right)^2\sigma_{x_1}^2 + \left(\frac{\partial f}{\partial x_2}\right)^2\sigma_{x_2}^2 + \left(\frac{\partial f}{\partial x_3}\right)^2\sigma_{x_3}^2 + \cdots}

Examples

For a function f=x+y, the propagated uncertainty can be shown to be \sigma_f^2=\sigma_x^2+\sigma_y^2

For equations of the form f=xy or f=x/y the propagated uncertainty is \left(\frac{\sigma_f}{f}\right)^2=\left(\frac{\sigma_x}{x}\right)^2+\left(\frac{\sigma_y}{y}\right)^2

A third useful result is when averaging many measurements \bar{x}=x_1+x_2+x_3+\cdots+x_N, where each measurement has an uncertainty \sigma_{x_i}. It can be shown that the uncertainty in the average is \sigma_{\bar{x}}=\frac{1}{N}\sqrt{\sum_{i=1}^N \sigma_{x_i}^2}