Objectives

1. Construct and plot a simulated wave packet that is localized in space
2. Show that decreasing the position uncertainty of the wave packet increases its momentum uncertainty

Resources

• Spreadsheet software (e.g. Microsoft Excel or Google Sheets)
• What is the Heisenberg Uncertainty Principle?

Background

Quantum mechanics asserts that all objects behave both as particles and waves. The De Broglie wavelength shows that an objects wavelength is inversely proportional to its momentum. \lambda=\frac{h}{mv}

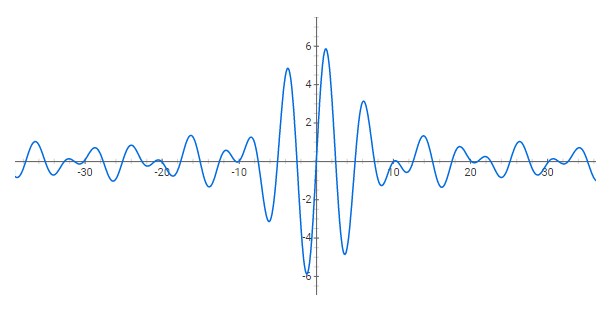
A wave packet is the sum of many waves of similar wavelengths, causing constructive superposition within a small region and destructive superposition outside it. Making the localized region smaller requires adding more wavelengths. This model is the basis of the Heisenberg Uncertainty Principle. \Delta_x \Delta_{p_x} = \hbar/2

 

Method

Use a spreadsheet program to create sine waves of different wavelengths and plot their sum. Adjust the number of waves, the wavelength range, and spread between wavelengths to create a localized wave packet.

Analysis Questions

1. How do you determine the “width” of your wave packet? Explain your criteria.
2. What is the relationship between the width and wavelength range of your wave packet? Give some quantitative results.
3. What distribution of wavelengths produces the best result? Try linear, quadratic, and exponential distributions.