Objectives

1. Show that angle of incidence equals angle of refraction for a flat mirror
2. Determine the radius of curvature of a concave and a convex mirror
3. Measure the index of refraction of a half-circular piece of glass
4. Predict and verify the critical angle that wil achieve total internal reflection in the glass

Resources

• Ray optics platform
• Ray optics light source
• Triangular mirror accessory with concave, convex and plane reflective surfaces
• Half-circular piece of glass
• Ruler

Background

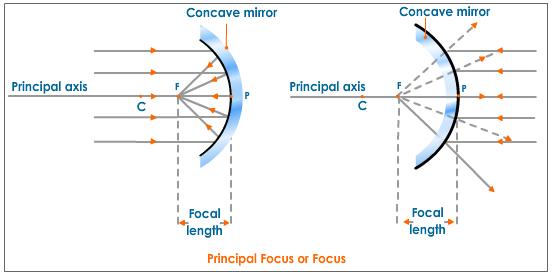
A light ray that strikes a reflective surface at an angle i to the normal will reflect at an angle r=i on the opposite side of the normal. Parallel light rays that strike a spherical, concave mirror with a radius of curvature R will thus all converge at a point F that is half this distance from the center of curvature, as shown in the diagram.

Refraction occurs because light travels at different speeds in different materials. The ratio between the speed of light in a material and its speed in a vacuum is the material’s index of refraction n. When a wavefront hits a boundary at an angle \theta_1, the wavefronts get closer or farther apart depending on the difference in wave speed. Because the particles that make up the wave are interacting, the parts of a wave (i.e. the crests and troughs) must stay in contact, which forces the wave to bend by an angle given by n_1 \sin\theta_1 = n_2\sin\theta_2

In the case where the light ray travels from a medium with a higher index of refraction to a medium with a lower one, it is possible for the refracted angle \theta_2 to be greater than ninety degrees, meaning light does not enter the second medium. This occurs at angles greater than or equal to the critical angle, given by \theta_c=\sin^{-1} \left( \frac{n_2}{n_1} \right)