Objectives

1. Measure the location of dark fringes in the pattern produced by shining a laser at a screen with single slits of varying widths.
2. Calculate the width of the slits based on the fringe locations.

Resources

• Optical bench
• Green diode laser
• mounted single-slit diffraction mask
• mounted screen
• ruler
• camera or phone

Background

When waves pass through the same point in space, they interfere with each other. They can cancel each other out or enhance each other at different points, depending on their relative phase and amplitude at a given position. The interference of light can be easily studied using a laser. Since a laser is essentially monochromatic, it produces regular interference patterns that can be easily observed.

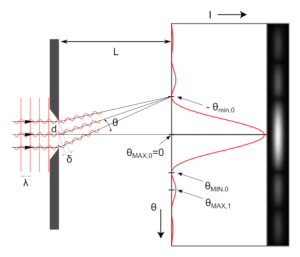
A pair of closely-spaced narrow slits can produce an interference pattern, but a single slit will produce an interference pattern as well. Compared to the double-slit interference pattern, a single-slit interference pattern has a wider central maximum, and the brightness of the adjacent maxima, or bright fringes, decreases more quickly.

The location of dark fringes produced by light of wavelength \lambda shining on a slit of width a, is given by a\sin\theta=m\lambda where m=0,1,2,\cdots denotes the m^{th} dark fringe of the interference pattern.

Setup

Set up the laser, slit mask, and screen on the optical bench as shown in the image above. Move the slit mask and screen as far apart as possible and record the distance. Adjust the slit mask so that the laser is hitting one of the single slits with a marked separation (a) of 0.02, 0.04, 0.08, or 0.16mm.

Suggested Method

Take a picture of the interference pattern on the screen and open it in an image editing program such as Microsoft Paint that will give you x,y pixel positions in the image. Measure the actual distance between the two most widely-spaced fringes you can see in the interference pattern, and compare this to their pixel spacing in the image to compute a pixels-to-meters scale. Use this scale to accurately measure the distance of as many dark fringes as you can from the brightest central fringe in the image.