String Wave Speed and Harmonics
Objectives
- Measure the wave speed on a string with a fixed tension and mass per unit length
- Test the relationship between harmonic number and wavelength for waves on a string of a given fundamental frequency
- Study how tension and string mass per unit length affect the speed of waves on a string
Resources
- Mechanical Vibrator
- String
- Clamp and Pulley
- Mass hanger and masses
- Meter Stick
- Frequency Generator
Background
For all waves, the relationship between the wavelength and frequency of the wave is v=\lambda f
where v is the speed at which the wave propagates through the medium. The wave speed itself is not affected by the wavelength or frequency of the wave, but depends on the physical properties of the medium. For waves propagating along a string of length L, mass m, and held taut with a force T, the wave speed can be shown to be v=\sqrt{\frac{T}{m/L}}
A wave that reflects between two fixed points, such as a sound wave in a pipe or a wave on a string stretched over a pulley, can produce standing waves if the distance between the fixed points is an integer multiple of the wavelength. The wavelength of the longest standing wave that is stable for a given system is called the fundamental, and each successively shorter wavelength is called the n^{th} harmonic, with a wavelength given by \lambda=\frac{2L}{n} Hint
Standing waves on a string provide a way for you to measure the wave velocity, since it you can see the wave shape and measure its wavelength.
Experimental Setup
The setup for this experiment consists of a string attached to a mechanical vibrator, which is driven by a frequency generator. Tension is maintained on the string by a mass attached to one end, which is draped over a pulley and allowed to hang. The tension on the string is thus T=mg. In order for the vibrations to have a large enough amplitude to see easily, a stretchy elastic string is used. For certain frequencies of vibration, the waves on the string will form a stable pattern called a standing wave, in which fixed points can be seen as shown below. This is useful since the wavelength can be easily measured, shown by L' in the example below.
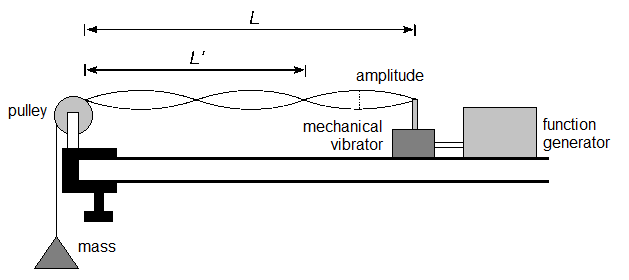
The mass m and length L of the string in the wave velocity equation above refer only to the part of the string that is vibrating, not the segment hanging vertically on the opposite side of the pulley. Additionally, the the string is stretched by different amounts depending on how much weight is added! This must be taken into account when calculating the wave speed from the tension and string mass per unit length.
