Tasks

1. Project images on a screen using a converging lens and determine its focal length.
2. Do the same for a diverging lens.
3. Build a very simple optical instrument: a Galilean telescope.

Resources

• Optical bench
• Light source
• Converging and diverging lenses and mounts
• Mounted white screen
• Ruler and/or meter stick

Background

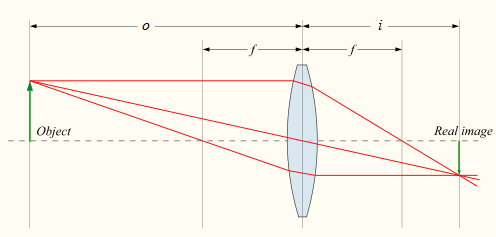
A thin lens is a piece of glass or transparent material with its faces curved in such a way that refraction causes light waves passing through it to focus to a point. This focusing of light allows clear images to be formed. The distance from a lens at which parallel incoming light rays are focused is defined as the lens’ focal length f. An object located a distance o from a lens of focal length f will produce an image at a distance i from the lens, according to the equation \frac{1}{o}+\frac{1}{i}=\frac{1}{f}

In this formula, o always has a positive value, and positive values of i give the position of a real image formed on the opposite side of the lens from an object, as shown in the diagram.

Negative image distances give a virtual image on the same side of the lens as the object. Such images cannot be focused on a screen, but can be seen at their calculated position by looking through the lens. Diverging lenses – those with two concave surfaces – have negative focal lengths and thus can only produce images on the same side of the lens as the object.

The apparent magnification of an object describes how much larger the image appears than the original object. It can be shown geometrically that this is related to the image and object distances. Negative magnifications mean an inverted image. m=-\frac{i}{o}

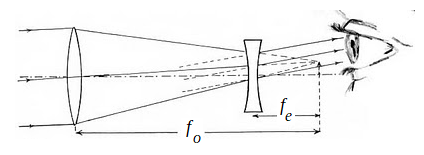
A simple optical instrument is the Galilean telescope. The purpose of a telescope is to focus and magnify parallel light rays from distant objects (e.g. stars) and return those focused rays to parallel so they can be easily viewed by the eye. A Galilean telescope uses a converging lens and a diverging lens as shown below. The magnification of a Galilean telescope is given by m=f_o/f_e, where f_e is the focal length of the eyepiece lens and f_o is the focal length of the objective.