Objectives

1. Show that the net force due to three hanging masses attached to a stationary ring in the center of the force table sum to zero, within the tolerance determined by your experimental precision/uncertainty.
2. Show that the net torque due to three hanging masses attached at different points to a horizontal disc supported by marbles on the force table sums to zero, within the tolerance of your experimental uncertainty.

Tools/Resources

• Force table with pulleys
• Circular plate with holes
• String, hooks and mass hangers
• Circular weights
• Steel or plastic balls, ~1cm diameter
• Phone or digital camera

Background

Understanding equilibrium is of vital importance for many professions from physicists and engineers to physical therapists. Knowledge of where forces and torques act in any equilibrium situation are important in determining whether a bridge will be stable or whether you will dislocate someone’s shoulder. The conditions for equilibrium of forces and torques are
\sum \vec{F} = \sum m_i \vec{a}_i = 0 \sum \vec{\tau} = \sum \vec{r}_i \times \vec{F}_i = 0

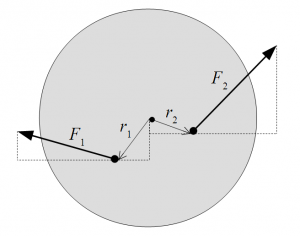Torque is a force that tends to cause angular acceleration of an object. Assuming an object’s rotation axis lies in the z-direction, the torque due to a force \vec{F} that is applied to an object at a distance \vec{r} from the rotation axis is \vec{\tau}=\vec{r}\times\vec{F}=(r_x F_y - r_y F_x)\hat{z}