Electron Charge-to-Mass Ratio
Tasks
- Use kinematics to estimate the acceleration needed to deflect an electron moving at speed v in an oscilloscope tube by an amount \Delta y.
- Use this model to estimate the charge-to-mass ratio of an electron.
Resources
- Oscilloscope (cathode ray tube style)
- Solenoid
- Power Supply
- Ruler
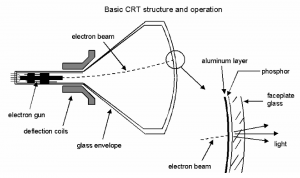 Background
Background
When the charge-to-mass ratio of the electron was first measured to be q/m \approx 1.76 \times 10^{11} \mathrm{C/kg}, it showed that the electron is in fact a particle with a mass and a charge. A cathode-ray tube is a device that creates a beam of electrons traveling at approximately 3 \times 10^{7}\ \textrm{m/s}.
The strength of the force a magnetic field B (usually measured in Teslas) exerts on a charge q moving with velocity v is F=qvB\sin\theta where \theta is the angle between the field and the charge’s direction of motion.
The magnetic field produced at the center of a solenoid (coil) of length L, number of turns N, with a current I running through it is B=\mu_0 \frac{N}{L} I where \mu_0 = 12.57 \times 10^{-7} \mathrm{T \cdot m / A}.
hint- A decent approximation for the solenoid is to assert that the magnetic field near the ends of the solenoid is uniform, constant, equal to the field at the center of the solenoid, and zero everywhere else.
- The effect of gravity upon on the electrons while they are in the beam of the CRT is negligible.