Objectives

For a damped simple harmonic oscillator system:

1. Determine the oscillation frequency
2. Measure the damping constant

Resources

• Spring
• Mass hanger and masses
• Square piece of cardboard that fits on mass hanger
• Motion sensor and computer software
• Rods and clamps for hanging spring

Background

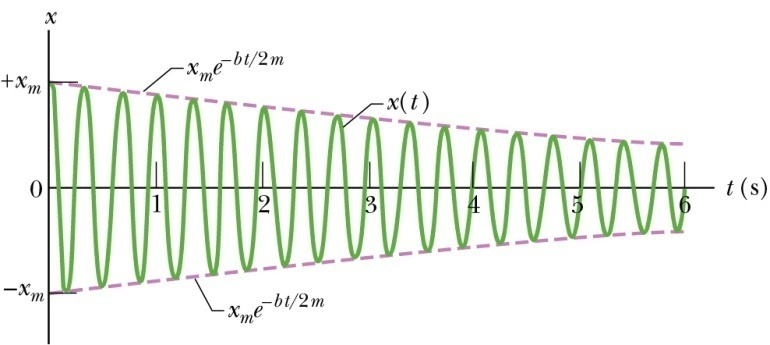
Any system that has a restoring force acting upon it can potentially produce simple harmonic motion. A mass m on a spring is one example, since the spring produces a restoring force of F=-kx on the mass, where k is the spring constant in units of Newtons/meter. Sometimes significant frictional/damping forces are present, causing the amplitude of the oscillations to decrease exponentially over time.

Damping forces are usually proportional to velocity, for example F=-bv where b is the damping constant. The equation describing the force on a damped harmonic oscillator is m\ddot{x} + b\dot{x} +kx = 0 The solution to this equation is x=x_m \cos(\omega t +\varphi)e^{-bt/2m}